Binary Trees Traversal Recursive vs. Iterative

Photo reference: https://computersciencewiki.org/index.php/Binary_tree

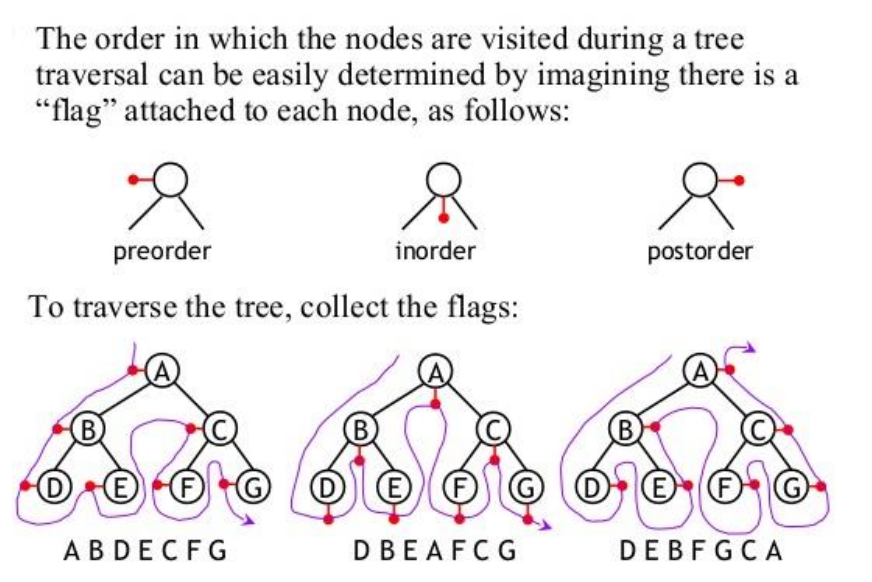
This neat little trick above saved me a lot of pain and is much quicker to get the traversals. Just think preorder = left, inorder = center, postorder = right. Then weave the string from the top left, to the bottom, to the center, and around until you get to the top right. Wherever the string would 'hook' into a line, write down that number as the next one in that type of traversal.

Given a binary tree, return the inorder traversal of its nodes' values.

Every recursive problem can be done iteratively using a stack. Recursive calls are simply utilizing the call stack that is an inherent part of the programming language. Don't forget to take into account the space the stack/recursive calls take up when doing the O notation for space!

Recursive solution:

public IList InorderTraversal(TreeNode root) 
{
	List result = new List();

	Helper(root, result);
	
	return result;
}

public void Helper(TreeNode root, List result)
{
	if (root == null) return;

	Helper(root.left, result);
	result.Add(root.val);
	Helper(root.right, result);
}

Time: O(n)
Space: O(log n) on average. O(n) worst case if tree is one giant linked list going in one direction.

Iterative solution using a stack:

public IList InorderTraversal(TreeNode root) 
{
	List result = new List();
	Stack stack = new Stack();
	
	TreeNode curr = root;
	
	while(curr != null || stack.Count != 0)
	{
		while(curr != null)
		{
			stack.Push(curr);
			curr = curr.left;
		}
		
		curr = stack.Pop();
		result.Add(curr.val);
		curr = curr.right;
	}
	
	return result;
}

Time: O(n)
Space: O(n)